page2

COMPACT, a tutorial by Scott W. Williams
title and preface	page 1: the beginnings	page 2: a special example
page3: functional separation	page4: the universe in a box	page5: open covers
References

2. A SPECIAL EXAMPLE

There are some special compact sets - the convergent sequence and its limit , the unit interval [0,1], and the unit circle. These tend to dominate how WE think of compact objects. The "long" space with an end-point is quite useful to However, the Cantor set is a fundamentally important compact object many people believe an aberration - it is not. Here's one reason why (Urysohn 1914):

2.1. THEOREM. Each compact metric space is the continuous image of the Cantor set.

THE CANTOR (MIDDLE-THIRDS) SET is the set of all real numbers the limit of an infinite series of the form , where each is 0 or 1. Note that if each =1 (=0), then the sum is 1 (0).

The construction of the Cantor Middle-Thirds Set proceeds recursively via removing various intervals from [0,1]:

Step1: From

remove the middle-third open interval (1/3 , 2/3) - we get a closed set, picture

C₁:

From both parts of C₁

remove the middle-third open interval - what's left is a closed set, picture

C₂:

From each of the four parts of

C₂:

remove the middle thirds open interval - picture

C₃:

And continue ...

The Cantor set is the intersection C =C_n. As an intersection of closed sets in [0,1], C is compact. As a closed subset of the compact set [0,1], C is closed, and hence, compact.

Noticing that the adjacent pairs in the Cantor C set can be mapped in an order preserving manner onto the rationals in (0,1). We see C can be pictured by considering [0,1] and replacing each rational number in (0,1) by two adjacent points. Indeed that picture gives impetus to a special case of Theorem 2.1 - [0,1] is the continuous image of C {just send adjacent points to one}.

Cantor Set

[0,1]

Concerning the Cantor set, one must be careful with intuition. First it is very thin, because the sum of the lengths of the deleted intervals is 1; i.e., its measure is zero. On the other hand it has the same size as the entire interval [0,1]. This is strengthened by the problem which appears in W. Rudin's textbook, and on some Ph.D. Qualifying Exams:

2.2. EXERCISE. Each real in the interval [0,2] is the sum of two members of the Cantor set:
For b[0,2]. Consider the graph L_b of the intersection of line x+y=b with subsets of the square [0,1]².

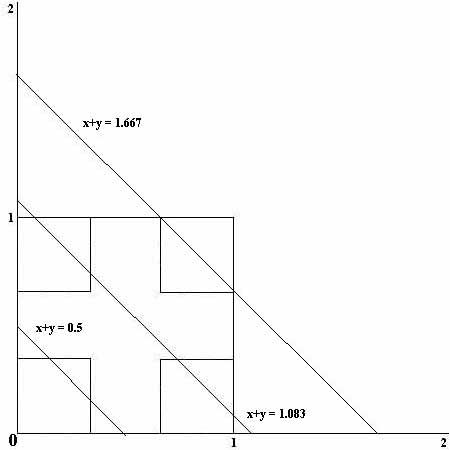
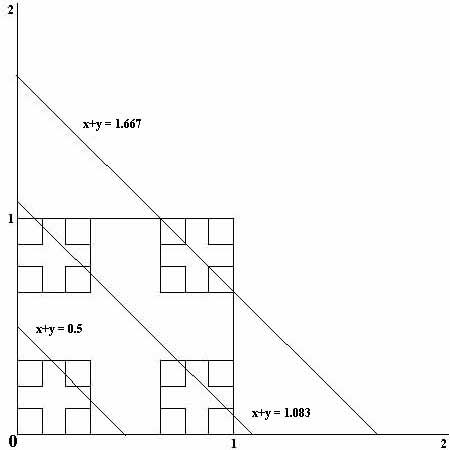
Indeed, each C_n²intersects L_b in a copy of some C_k. Thus,
L_bC²=(L_bC_n²) is not empty; i.e., there are elements x and y in the Cantor set such that x+y=b.

In 1999 the great topologist Mary Ellen Rudin solved an outstanding problem generalizing 2.1, which asked for a kind of "triangular inequality" extension of metric. She proved the hard "sufficient" in:

2.3. THEOREM. In order for a compact space X to be the continuous image of a compact linear ordered space it is necessary and sufficient that for each pair consisting of a point xX and its neighborhood G, there exists an open set G_x satisfying two conditions:

1. xG_xG.

2. If G_xH_y , then either yG or xH.

A pre-print of the paper Nikiel's problem is available at the web site of the journal TOPOLOGY ATLAS (http://at.yorku.ca/topology/)

{Note. The "trianguar inequality" comment is motivated by observing that in a metric space when G is the open ball about x of radius r, we may take G_x to be the open ball about x of radius r/3. Then the triangular inequality proves condition (2)}

title and preface	page 1: the beginnings	page 2: a special example	page3: functional separation
page4: the universe in a box		page5: open covers	References