page1
1. the beginnings
The Cech Mathematician Bernard Bolzano did
a number of remarkable things very early. In particular, in 1817,
he extacted numbers from the notion of sequence [Kline1972], and gave early formulation of finite and infinite
sets [Cantor
1883, Jarnik1981]. In the 1830's he showed that a function continuous
on a closed interval is bounded, proved that a bounded sequence
has a limit point [Bolzano1841,
Jarnik1981], and gave the first example of a continuous nowhere
differentiable function (usually attributed to Weierstrass 30
years later). The proof of these essentially led to the Bolzano-Weierstrass
Theorem [Taylor
1982]:
1.1. THEOREM. Every infinite bounded subset of reals has a limit
point.
A key to this theorem is an axiom implying
that the real line has "no holes except at infinity":
Call the set B.
If B contains an
infinite increasing sequence, then the least upper bound of the
sequence is a limit point. The infinite decreasing sequence case
is analogous. By a partitioning B, we see that a bounded set without monotone infinite
sequences must be finite.
Before the 19th century, folks already knew
that "small" polynomials attained their maxima and minima
on closed intervals, but the Bolzano-Weierstrass Theorem led to
what turns out to be one of the chief motivations for studying
compactness, Weierstrass' theorem [Taylor 1982]:
1.2. THEOREM. Each function continuous on a closed subset of a closed
interval attains its maximum.
The essence is that the continuous image of
a closed and bounded set is closed and bounded. Today we know
Theorem2 to be true for real-vlaued functions continuous on any
compact space; however, theorems 1.1 and 1.2 suggest:
1.3. DEFINITION. COMPACT = "NO HOLES": This should be interpreted
intuitively. The "proofs" we give in 1.4 are intuitive
and need either to be fleshed out with the definition given in
1.5 or 5.1.
1.4. EXERCISES.
1. We
recognize two possible kinds of holes - holes at infinity and
holes nearby.
a. Loosely, compactness requires a kind of
boundedness.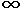 
is
a hole of the non-negative integers {0,1,2,3,4
...} is not compact. When the hole at
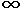is put in - considering
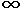as a point, the
new object, 
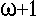, has
no holes.
b. Compactness, loosely, requires a special
kind of "closedness." 0 is a hole of the "convergent"
sequence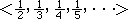 
and
the sequence, without its limit, is not compact. With its limit,
it is compact. More generally, if (0,1] with its usual open sets is declared closed in some
topology on the line, then [0,1] is not compact in that topology.
2. Removing the origin <0,0> from the
unit disk also leaves a nearby hole:
Thus,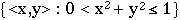 
is not compact.
3. Intutitively, "hole" implies
some kind of an unending process without resolution. So intutively,
finite sets are compact.
4. Suppose * is a hole of a closed
subset F of a compact
space X. As a there
is stuff of F "close
to" *, there is stuff of X "close to" *. But X is compact and * must be a point of X. Since F
is a closed subset of X,
it contains all points of X close to it. So, a closed subset of a compact
set must be compact.
5. A far away hole: The
space 
of all countable ordinal numbers has no holes approachable
by a countable sequence, yet is not compact.
When a point has been put in the hole, the
space is known as 
.
1.5. DEFINITION. A filter is a family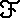 
of non-empty sets which satisfy the condition: If
A,B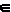
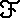, then there is a C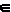 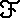contained in A
B.
Here is a correct definition of "close
to": 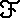converges to (clusters
at) the point x
provided each neighborhood of x contains (intersects) a member of .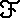
Here is a correct definition of compact: A
space is said to be compact provided each filter consisting of closed sets is
contained in a converent filter; or equivalently, each filter
consisting of closed sets clusters at some point.
This version of compactness was important since
the 1940's, but is related to the first study of abstract compact
spaces [Vietoris1921].
copy permission each person is allowed one electronic version
of this paper and one hard copy printout.
